Oi galera. Estava pesquisando em alguns sites e encontrei essas dicas interessantes no somatematica.com. Espero que vocês gostem. Beijos...
DICA 1: Multiplicar um número por 10:
Basta deslocar a vírgula uma casa decimal para a direita.Exemplo 1: 16 x 10 = 160Exemplo 2: 15,567 x 10 = 155,67
DICA 2: Multiplicar um número por 10n:
Basta deslocar a vírgula n casas decimais para a direita.Exemplo 1: 16 x 103 = 16000Exemplo 2: 15,567 x 104 = 155670
Então, se quisermos efetuar a seguinte multiplicação: 12 x 100. Sabemos que 100=102, então:12 x 100 = 12 x 102 = 1200.
DICA 3: Dividir um número por 10:
Basta deslocar a vírgula uma casa decimal para a esquerda.Exemplo 1: 16 / 10 = 1,6Exemplo 2: 15,567 / 10 = 1,5567
DICA 4: Dividir um número por 10n:
Basta deslocar a vírgula n casas decimais para a esquerda.Exemplo 1: 16 / 103 = 0,016Exemplo 2: 15,567 / 102 = 0,15567
Então, se quisermos efetuar a seguinte divisão: 12 / 1000. Sabemos que 1000=103, então:12 / 1000 = 12 / 103 = 0,012.
DICA 5: Multiplicar um número por 11:
Quando o número for de 2 algarismos, basta somar esses 2 algarismos e colocar o resultado no meio deles. Por exemplo, vamos efetuar a seguinte multiplicação: 26 x 11.
Temos o número 26, somando seus 2 algarismos temos 2+6=8. Pronto! Agora é só colocar esse 8 no meio deles:a resposta é 286. Portanto 26 x 11 = 286.
Outros exemplos:
1) 34 x 11somamos os algarismos do número 34: 3+4=7colocamos o resultado no meio deles: 374. Portanto 34x11 = 374.
2) 81 x 11somamos os algarismos do número 81: 8+1=9colocamos o resultado no meio deles: 891. Portanto 81x11 = 891.
3) 37 x 11somamos os algarismos do número 37: 3+7=10
Como deu um nº maior que 9, então não podemos colocar todo o número no meio deles. Colocamos apenas o algarismo das unidades (0) no meio deles, e o algarismo da dezena (1) é somado ao primeiro algarismo do número: 407. Portanto 37x11 = 407.
Quando o número for de 3 algarismos, então esse número multiplicado por 11 resultará em um número de 4 algarismos. Por exemplo, vamos efetuar a seguinte multiplicação: 135 x 11.
Temos o número 135. Somando o 1º com o 2º algarismo desse número temos 1+3=4. Somando o 2º com o 3º algarismo desse número temos 3+5=8. Esses 2 resultados serão colocados no meio do número 135, tirando o seu algarismo do meio:1485. Portanto 135 x 11 = 1485.
DICA 6: Multiplicar um número por 9:
Nesse caso basta acrescentar um zero no final do número e subtrair pelo número inicial. Vamos efetuar a seguinte multiplicação: 44 x 9.
Acrescentando um zero no final do número 44 ficamos com 440.Então subtraímos desse valor o valor inicial: 440-44 = 396.Portanto 44 x 9 = 396.
Outros exemplos:27 x 9 = 270-27 = 243.56 x 9 = 560-56 = 504.33 x 9 = 330-33 = 297.
DICA 7: Multiplicar um número por 99:
Nesse caso basta acrescentar 2 zeros no final do número e subtrair pelo número inicial. Vamos efetuar a seguinte multiplicação: 44 x 99.
Acrescentando 2 zeros no final do número 44 ficamos com 4400.Então subtraímos desse valor o valor inicial: 4400-44 = 4356.Portanto 44 x 99 = 4356.
Outros exemplos:27 x 99 = 2700-27 = 267356 x 99 = 5600-56 = 554433 x 99 = 3300-33 = 3267
DICA 8: Multiplicar um número por 101:
Quando um número de 2 algarismos AB for multiplicado por 101, o resultado será ABAB. Alguns exemplos:
43 x 101 = 434332 x 101 = 323214 x 101 = 1414
DICA 9: Multiplicar 2 números (de 2 algarismos) que possuam o mesmo algarismo das dezenas, e a soma de seus algarismos das unidades seja 10.
Exemplos de multiplicações que podem ser feitas com esse método: 42x48, 53x57, 21x29, 35x35, 87x83, 94x96, etc.
Devem ser seguidos os seguintes passos:
1) Multiplicamos o algarismo das dezenas (que é igual nos 2 números) pelo número seguinte a ele;
2) Multiplicamos os algarismos das unidades normalmente;
3) Juntamos as duas partes.
Vamos efetuar a seguinte multiplicação: 53 x 57:
Passo 1:5x6 = 30
Passo 2:3x7 = 21
Passo 3:Juntamos os dois números: 3021.Portanto 53 x 57 = 3021. Barbada!
Outro exemplo: 94 x 96:
Passo 1:9x10 = 90
Passo 2:4x6 = 24
Passo 3:Juntamos os dois números: 9024.Portanto 94 x 96 = 9024. Barbada!
DICA 10: Soma dos n primeiros números naturais ímpares:
A soma dos n primeiros números naturais ímpares é igual a n2. Exemplos:
1) Soma dos 5 primeiros números naturais ímpares (1+3+5+7+9):A soma é igual a 52 = 25.
2) Soma dos 15 primeiros números naturais ímpares:A soma é igual a 152 = 225.
DICA 11: Multiplicar um número por 15:
Some o número com a sua metade, e multiplique o resultado por 10.Exemplos: 14×15 =(14+7)×10=21010,4×15=(10,4+5,2)×10=15,6×10=156
DICA 12: Tabuada do 9:
Se você tem dificuldades para decorar a tabuada do 9, pode fazer o seguinte:
1) Considere o número anterior ao qual você irá multiplicar o 9.
2) Veja quanto falta para ele chegar ao 9.
3) Junte os dois números encontrados.
Por exemplo:
1) 9 x 2 => o número anterior ao dois é o 1.
2) Para o 1 chegar ao 9, faltam 8.
3) Agora basta unir os dois números: 18
Portanto, 9 x 2 = 18.
Da mesma forma pode ser feito para os outros números, até chegar em 9x9:
1) 9 x 9 => o número anterior ao nove é o 8.
2) Para o 8 chegar ao 9, falta 1
3) Agora basta unir os dois números: 81
Portanto, 9 x 9 = 81.
DICA 13: Dividir qualquer número por 5:
Basta multiplicar o número por 2 e "arrastar" a vírgula para a esquerda.
Ex: 345 / 5 = 345 * 2 = 690. Arrastando a vírgula, temos 69,0.
Ex: 1526 / 5 = 1526 * 2 = 3052. Arrastando a vírgula, temos 305,2.
DICA 14: Como descobrir o próximo quadrado?
Some o quadrado anterior com duas vezes com o número do qual você quer descobrir o quadrado, e depois diminua uma unidade.
Ex: Se 32=9, quanto vale 42?
Aplicando a regra, temos: 9 + 4 + 4 = 17
17 - 1 = 16
Portanto, 42 = 16
Outro exemplo: 52 = ?
16 + 5 + 5 - 1 = 25
DICA 15: Adição: Arredondamento da 2ª parcela para um múltiplo de 10 conveniente:
Arredonda-se a 2ª parcela para o 1ª múltiplo de 10 inferior a esse número. Posteriormente, acrescenta-se a diferença entre o número original e o número arredondado. Exemplos:
23 + 36 = 23 + 30 + 6 = 53 + 6 = 59
357 + 459 = 357 + 450 + 9 = 807 + 9 = 816
Observação: Quando for conveniente, arredonda-se a 2ª parcela para o 1ª múltiplo de 10 superior a esse número. Posteriormente, subtrai-se a diferença entre o número arredondado e o número original.
Exemplo:
357 + 459 = 357 + 460 - 1 = 817 – 1 = 816
quinta-feira, 24 de setembro de 2009
segunda-feira, 7 de setembro de 2009
A MATEMÁTICA E AS PROFISSÕES.
A Matemática faz parte de quase todas as profissões. Confira na listagem abaixo as aplicações da Matemática em algumas das profissões mais tradicionais.
Administração
A administração requer muito planejamento, organização e controle. Portanto, é indispensável que o administador tenha habilidade em lidar com números. Muitas vezes ele deverá preparar orçamentos para projetos, planejar e controlar pesquisas, além de resolver situações que envolvam cálculos estatísticos. O trabalho do administrador está diretamente ligado com a exatidão dos números, e por isso ele precisa ter domínio da matemática para ser bem sucedido.
Agronomia
Cálculo dos componentes químicos destinados à fertilização e dimensionamento das áreas a serem cultivadas.
Arquitetura
A matemática é fundamental para que o arquiteto possa desenvolver o seu trabalho. O arquiteto trabalha na construção de casas, edifícios, reformas, restaurações e no planejamento de bairros e cidades. A arquitetura é uma união das áreas de exatas, humanas e arte, pois exige aptidões múltiplas, como o domínio de cálculos, desenhos intuitivos e história.
Cinema
Muitas animações que vemos no cinema utilizam a Matemática, através da computação gráfica. Desde o movimento dos personagens até o quadro de fundo podem ser criados por softwares que combinam pixels em formas geométricas, que são armazenadas e manipuladas. Os softwares codificam informações como posição, movimento, cor e textura de cada pixel. Para isso, utilizam vetores, matrizes e aproximações poligonais de superfícies para determinar a característica de cada pixel. Um simples quadro de um filme criado no computador tem mais de dois milhões de pixels, o que torna indispensável o uso de computadores para realizar todos os cálculos necessários.
Direito
O profissional do Direito utiliza a Matemática quando trabalha com causas que envolvam a realização de cálculos, como por exemplo bens, valores, partilhas e heranças.
Engenharia
A matemática é imprescindível à formação dos engenheiros, seja qual for o seu ramo (engenharia civil, engenharia elétrica etc). É usada na construção de edifícios, estradas, túneis, metrôs, ferrovias, barragens, portos, aeroportos, usinas, sistemas de telecomunicações, criação de dispositivos mecânicos, desenvolvimento de máquinas, entre outros.
Geologia
O geólogo utiliza diversos princípios da Matemática para escavar, conhecer e avaliar os segredos do solo e das pedras.
Jornalismo
A Matemática é útil aos jornalistas de economia e política, além daqueles que utilizam dados estatísticos em seus trabalhos.
Odontologia
O dentista utiliza a Matemática para calcular composições de amálgamas, posologias, doses de anestésicos e também para dimensionar próteses e aparelhos corretivos.
Psicologia
O psicólogo utiliza a Matemática para a análise de dados estatísticos e avaliação de testes.
Ë isso aí pessoal, a Matemática está presente em tudo mesmo. Em breve colocarei outras profissões...
Administração
A administração requer muito planejamento, organização e controle. Portanto, é indispensável que o administador tenha habilidade em lidar com números. Muitas vezes ele deverá preparar orçamentos para projetos, planejar e controlar pesquisas, além de resolver situações que envolvam cálculos estatísticos. O trabalho do administrador está diretamente ligado com a exatidão dos números, e por isso ele precisa ter domínio da matemática para ser bem sucedido.
Agronomia
Cálculo dos componentes químicos destinados à fertilização e dimensionamento das áreas a serem cultivadas.
Arquitetura
A matemática é fundamental para que o arquiteto possa desenvolver o seu trabalho. O arquiteto trabalha na construção de casas, edifícios, reformas, restaurações e no planejamento de bairros e cidades. A arquitetura é uma união das áreas de exatas, humanas e arte, pois exige aptidões múltiplas, como o domínio de cálculos, desenhos intuitivos e história.
Cinema
Muitas animações que vemos no cinema utilizam a Matemática, através da computação gráfica. Desde o movimento dos personagens até o quadro de fundo podem ser criados por softwares que combinam pixels em formas geométricas, que são armazenadas e manipuladas. Os softwares codificam informações como posição, movimento, cor e textura de cada pixel. Para isso, utilizam vetores, matrizes e aproximações poligonais de superfícies para determinar a característica de cada pixel. Um simples quadro de um filme criado no computador tem mais de dois milhões de pixels, o que torna indispensável o uso de computadores para realizar todos os cálculos necessários.
Direito
O profissional do Direito utiliza a Matemática quando trabalha com causas que envolvam a realização de cálculos, como por exemplo bens, valores, partilhas e heranças.
Engenharia
A matemática é imprescindível à formação dos engenheiros, seja qual for o seu ramo (engenharia civil, engenharia elétrica etc). É usada na construção de edifícios, estradas, túneis, metrôs, ferrovias, barragens, portos, aeroportos, usinas, sistemas de telecomunicações, criação de dispositivos mecânicos, desenvolvimento de máquinas, entre outros.
Geologia
O geólogo utiliza diversos princípios da Matemática para escavar, conhecer e avaliar os segredos do solo e das pedras.
Jornalismo
A Matemática é útil aos jornalistas de economia e política, além daqueles que utilizam dados estatísticos em seus trabalhos.
Odontologia
O dentista utiliza a Matemática para calcular composições de amálgamas, posologias, doses de anestésicos e também para dimensionar próteses e aparelhos corretivos.
Psicologia
O psicólogo utiliza a Matemática para a análise de dados estatísticos e avaliação de testes.
Ë isso aí pessoal, a Matemática está presente em tudo mesmo. Em breve colocarei outras profissões...
segunda-feira, 31 de agosto de 2009
JOGOS DE TABULEIRO DO 7o ANO
Ao término do 2o bimestre, os alunos do 7o ano fizeram um trabalho em grupo no qual eles tinham que montar um jogo de tabuleiro.
Nesse jogo, o que determina a quantidade de "casas" que o jogador deve andar é o resultado de uma equação, seja ela simples ou de um sistema de equações.
As equações foram montadas por eles e, eu auxiliei para que as respostas fossem possíveis para avançar ou retroceder cada peão no tabuleiro.
O formato do tabuleiro foi determinado pelo grupo e os "peões" foram feitos por eles.
Cada jogo tinha que ter o manual de como jogar e as regras tinham que estar estabelecidas, assim como o número mínimo e máximo de jogadores.
O resultado foi maravilhoso!
Aí vão algumas fotos dos grupos e dos tabuleiros.
Quem se interessar em jogá-los, é só aparecer na escola e solicitar o jogo que mais lhe agrada e, BOA SORTE!!!



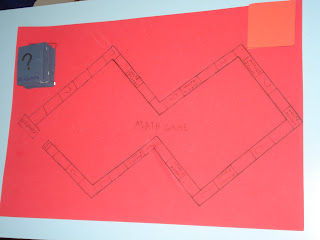



Nesse jogo, o que determina a quantidade de "casas" que o jogador deve andar é o resultado de uma equação, seja ela simples ou de um sistema de equações.
As equações foram montadas por eles e, eu auxiliei para que as respostas fossem possíveis para avançar ou retroceder cada peão no tabuleiro.
O formato do tabuleiro foi determinado pelo grupo e os "peões" foram feitos por eles.
Cada jogo tinha que ter o manual de como jogar e as regras tinham que estar estabelecidas, assim como o número mínimo e máximo de jogadores.
O resultado foi maravilhoso!
Aí vão algumas fotos dos grupos e dos tabuleiros.
Quem se interessar em jogá-los, é só aparecer na escola e solicitar o jogo que mais lhe agrada e, BOA SORTE!!!







quinta-feira, 13 de agosto de 2009
EQUAFUNK
Oi pessoal.
No dia 20 de maio, quando dava aula sobre "Equações de 1o grau", resolvi fazer uma paródia da música "Dança do quadrado" o que foi muito bem aceito pelos alunos.
Depois de alguns dias pensando, saiu algo assim:
Separa a variável do termo independente (2x)
Variável no primeiro membro (2x)
Independente no segundo membro (2x)
Se tiver que mudar de membro, carrega a operação inversa (2x)
Resolva a operação indicada em cada membro (2x)
Finaliza com a divisão (2x)
Verifique a solução (2x)
É, você mostrou como é que é..."
No dia 20 de maio, quando dava aula sobre "Equações de 1o grau", resolvi fazer uma paródia da música "Dança do quadrado" o que foi muito bem aceito pelos alunos.
Depois de alguns dias pensando, saiu algo assim:
EQUAFUNK
"Primeiro organiza (4x)Separa a variável do termo independente (2x)
Variável no primeiro membro (2x)
Independente no segundo membro (2x)
Se tiver que mudar de membro, carrega a operação inversa (2x)
Resolva a operação indicada em cada membro (2x)
Finaliza com a divisão (2x)
Verifique a solução (2x)
É, você mostrou como é que é..."
O nome foi escolhido pelos alunos do 7o ano da Dinâmica e eu contei com a ajuda das "DRIQUETES" Ana Helena e Lorenna para apresentar a música para toda a sala.
Espero que gostem...
Assinar:
Comentários (Atom)


